Video: Cum găsiți forma componentei unui vector având în vedere mărimea și unghiul?
2024 Autor: Miles Stephen | [email protected]. Modificat ultima dată: 2023-12-15 23:40
VIDEO
Ținând cont de acest lucru, este 0 un vector unitar?
A vector unitar este o vector care are o magnitudine de 1. Notația reprezintă norma, sau mărimea, a vector v. De bază vectori unitari sunt i = (1, 0 ) și j = ( 0 , 1) care au lungimea 1 și au direcții de-a lungul axei x pozitive și, respectiv, a axei y.
În plus, cum arată forma componentei? The forma componentei a unui vector este perechea ordonată care descrie modificările valorilor x și y. În graficul de mai sus x1=0, y1=0 și x2=2, y2=5. Doi vectori sunt egale dacă au aceeași mărime și direcție. ei sunt paralele dacă au aceeaşi direcţie sau opusă.
În plus, ce înțelegeți prin magnitudine?
În fizică, magnitudinea înseamnă măreție de dimensiune sau întindere. Un vector are a magnitudinea și o direcție, ea magnitudinea fiind valoarea numerică a lungimii, mărimii sau cantității sale. Un scalar în fizică este definit de magnitudinea sau cantitate și nu după direcție.
Cum afli mărimea și unghiul unui vector?
- Aplicați ecuația. pentru a găsi magnitudinea, care este 1,4.
- Aplicați ecuația theta = tan–1(y/x) pentru a afla unghiul: tan–1(1,0/–1,0) = –45 grade. Cu toate acestea, rețineți că unghiul trebuie să fie într-adevăr între 90 de grade și 180 de grade, deoarece prima componentă vectorială este negativă, iar a doua este pozitivă.
Recomandat:
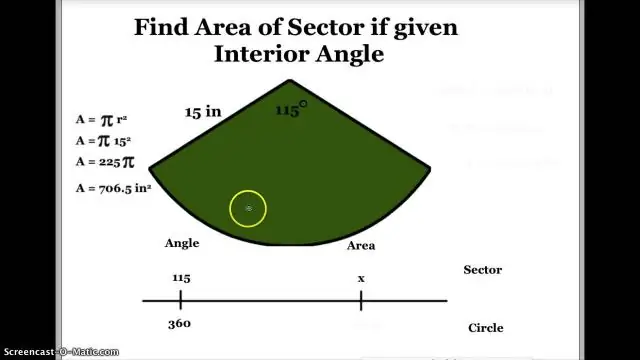
Cum găsești unghiul central având în vedere aria și raza unui sector?
Determinarea unghiului central din zona sectorului (πr2) × (unghiul central în grade ÷ 360 grade) = aria sectorului. Dacă unghiul central se măsoară în radiani, formula devine în schimb: aria sectorului = r2 × (unghiul central în radiani ÷ 2). (θ ÷ 360 grade) × πr2. (52,3 ÷ 100π) × 360. (52,3 ÷ 314) × 360
Cum găsiți mărimea formei componentei?
Mărimea unui vector dat sub formă de componentă este dată de rădăcina pătrată a sumei pătratelor fiecărei componente a vectorului. adică dat un vector V(p, q), mărimea vectorului este dată de |V| = sqrt(p^2 + q^2)
Cum scrieți o ecuație sub formă de panta punctuală având în vedere două puncte?
Există diferite forme în care putem scrie ecuația unei drepte: forma punct-pantă, forma panta-intersecție, forma standard etc. Ecuația unei drepte având două puncte (x1, y1) și (x2, y2) ) prin care trece linia este dată de, ((y - y1)/(x - x1)) / ((y2 - y1)/(x2 - x1))
Cum găsiți ecuația unei drepte având în vedere un punct și o dreaptă paralelă?
Ecuația dreptei în forma pantei-intersecție este y=2x+5. Panta paralelei este aceeași: m=2. Deci, ecuația dreptei paralele este y=2x+a. Pentru a găsi a, folosim faptul că linia ar trebui să treacă prin punctul dat:5=(2)⋅(−3)+a
Cum găsiți unghiul unui sector într-o diagramă circulară?
1 Răspuns În orice sector, există 3 părți care trebuie luate în considerare: Lungimea arcului este o fracțiune din circumferință. Aria sectorului este o fracțiune din întreaga zonă. Acest unghi sector este o fracțiune de 360° Dacă sectorul reprezintă 20% din diagrama circulară, fiecare dintre aceste părți este 20% din total. 20%×360° 20100×360=72°