Cuprins:
Video: Cum folosești regula pentru mâna dreaptă pentru produsul încrucișat?
2024 Autor: Miles Stephen | [email protected]. Modificat ultima dată: 2023-12-15 23:40
The dreapta - regulă de mână afirmă că orientarea vectorilor' produs încrucișat se determină prin plasarea și coadă la coadă, aplatizarea mana dreapta , extinzându-l în direcția, și apoi onduland degetele în direcția pe care o face unghiul cu. The deget mare apoi indică în direcția.
Doar așa, cum faci regula mânii corecte pentru produsul încrucișat?
The produs încrucișat va fi întotdeauna un alt vector care este perpendicular pe ambii vectori originali. Direcția produs încrucișat se găsește folosind regula dreapta , în timp ce amploarea produs încrucișat este dat de: Cuplul este tendința unei forțe de a face ca un obiect să se rotească.
care este regula produselor încrucișate? The produs încrucișat a × b este definit ca a vector c care este perpendiculară (ortogonală) atât pe a cât și pe b, cu o direcție dată de mâna dreaptă regulă și o magnitudine egală cu aria paralelogramului pe care o întind vectorii.
Cineva se poate întreba, de asemenea, cum folosiți regula mâinii drepte?
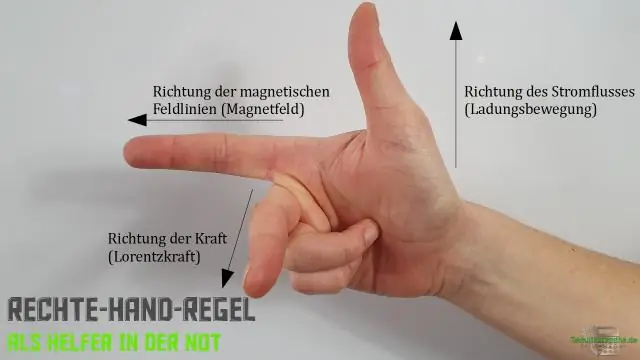
Direcția produsului încrucișat poate fi găsită prin aplicarea regulii mâinii drepte, după cum urmează:
- Degetul arătător indică în direcția vectorului vitezăv.
- Degetul mijlociu indică în direcția câmpului magnetic vector B.
- Degetul mare este îndreptat în direcția produsului încrucișat F.
Cum se calculează produsul încrucișat?
Noi putem calculati cel Produs încrucișat astfel: Deci lungimea este: lungimea a ori lungimea de b ori sinusul unghiului dintre a și b, apoi înmulțim cu vectorul n pentru a ne asigura că se îndreaptă în direcția corectă (în unghi dreptunghic atât la a cât și la b).
Recomandat:
Ce este produsul încrucișat și punctual?
Produsul punctual, interacțiunile dintre dimensiuni similare (x*x, y*y, z*z) Produsul încrucișat, interacțiunile dintre diferite dimensiuni (x*y, y*z, z*x etc.)
Cum folosești regula produs și coeficient?
Regula produsului spune că derivata unui produs a două funcții este prima funcție înmulțită cu derivata celei de-a doua funcții plus a doua funcție înmulțită cu derivata primei funcții. Regula produsului trebuie utilizată atunci când se ia derivata coeficientului a două funcții
De unde știi când să folosești produsul sau regula coeficientului?
Împărțirea funcțiilor. Deci, ori de câte ori vedeți înmulțirea a două funcții, utilizați regula produsului și în cazul împărțirii folosiți regula coeficientului. Dacă funcția are atât înmulțirea, cât și împărțirea, utilizați ambele reguli în consecință. Dacă vedeți o ecuație generală, este ceva de genul,, unde este o funcție în termeni de singur
Cum convertiți regula coeficientului în regula produsului?
Regula coeficientului ar putea fi văzută ca o aplicare a regulilor produsului și lanțului. Dacă Q(x) = f(x)/g(x), atunci Q(x) = f(x) * 1/(g(x)). Puteți folosi regula produsului pentru a diferenția Q(x), iar 1/(g(x)) poate fi diferențiat folosind regula lanțului cu u = g(x) și 1/(g(x)) = 1/u
Ar avea sens să găsim ecuația unei drepte paralele cu o dreaptă dată și printr-un punct de pe dreapta dată?
Ecuația unei drepte care este paralelă sau perpendiculară pe o dreaptă dată? Răspuns posibil: Pantele dreptelor paralele sunt egale. Înlocuiți panta cunoscută și coordonatele unui punct de pe cealaltă dreaptă în forma punct-pantă pentru a găsi ecuația dreptei paralele